Querying large datasets can often be challenging, especially when performance is a key concern. Achieving performance at scale often comes with an element of trade-off in how a system is designed to achieve the desired functionality and performance at scale.
A bloom filter is one example of a probabilistic data structure that is designed to answer the question: "have I seen this item before"?
Interesting Use Cases
Here are a few quick examples of interesting use cases for a Bloom Filter.
- Google Safe Browsing
Google Chrome used a bloom filter to determine if a website a user was about to visit was malicious without needing to distribute a large database of malicious URLs or make external API calls to determine the maliciousness of a URL. - Akamai Cache Performance
Akamai determined that their Content Delivery Network (CDN) cache was saturated with "one-hit-wonders" (web pages that were only ever accessed once). Akamai switched to using a bloom filter to determine if a page had been accessed more than once and only to cache a page if it had been accessed at least once before. This avoids the cache being populated with "one-hit-wonders" and freed up 75% of their cache. - Articles You've Read
Medium uses a bloom filter as a performant mechanism for determining if a user has read an article before.
We will explore each of these use cases in detail, but first, let's take a look at how a bloom filter works.
What is a Bloom Filter?
A bloom filter is a space-efficient probabilistic data structure that is designed to answer the question:
Is a given element a member of a set?
A bloom filter will answer this in one of two ways:
- Definitely No – a bloom filter is 100% accurate in identifying that an element is not part of the set.
- Probably Yes – a bloom filter can determine to a high degree of accuracy that an element probably does exist, but it can sometimes return yes even though the element is not a member of the set.
This "probably yes" quality of a bloom filter is why a bloom filter is considered a probabilistic data structure. With a bloom filter, our dataset is encoded in a space-efficient way. Whilst this will use significantly less space than if we had a fully-fledged database, this has the tradeoff of reduced accuracy.
Probabilistic or statistical data models are often assessed in terms of:
- True Positive (TP) – a true positive is where a model accurately predicts that something happened (e.g. the member is an element of the set)
- False Positive (FP) – a false positive is where a model predicts that something happened when it didn't (e.g. the member is an element of the set, but in reality, it isn't)
- True Negative (TN) – a true negative is when a model accurately predicts that something did not happen (e.g. the member is not an element of the set)
- False Negative (FN) – a false negative is when a model predicts that something didn't happen when it did (e.g. the member is not an element of the set when, in reality, it is)
A bloom filter has the following characteristics:
| Predicted Negative | Predicted Positive | |
|---|---|---|
| Actual Negative |
True Negative (TN) The member is not an element of the set Probability: 100% |
False Positive (FP) The member is an element of the set, but in reality, it isn't Probability: >0% |
| Actual Positive |
False Negative (TN) The member is not an element of the set Probability: 0% |
True Positive (TP) The member is not an element of the set when in reality, it is Probability: <100% |
The table above (known as a confusion matrix) shows that a false negative isn't possible. This is why we can be certain that if the bloom filter says "no", it's definitely a no.
On the other hand, there is a false positive rate with a bloom filter, which is why a "yes" is probably yes. The accuracy of a bloom filter will depend on how we have configured the filter and how much space it requires. A filter that has been configured to use more space will have a higher accuracy than one that has been configured to use less space.
How Does a Bloom Filter Work?
A bloom filter uses an array of bits and a series of hash functions to answer the question, "Is a given element a member of the set?".
An empty bloom filter will consist of a bit array of a particular length (which we will call w), where all bits are initially set to 0:
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Bit Value | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
When a bloom filter needs to evaluate if an element is a member of the set, it will use a series of hashing functions to determine which bits to check in the bloom filter. If these bits are already set to 1, then this would indicate that the bloom filter has probably already seen this element.
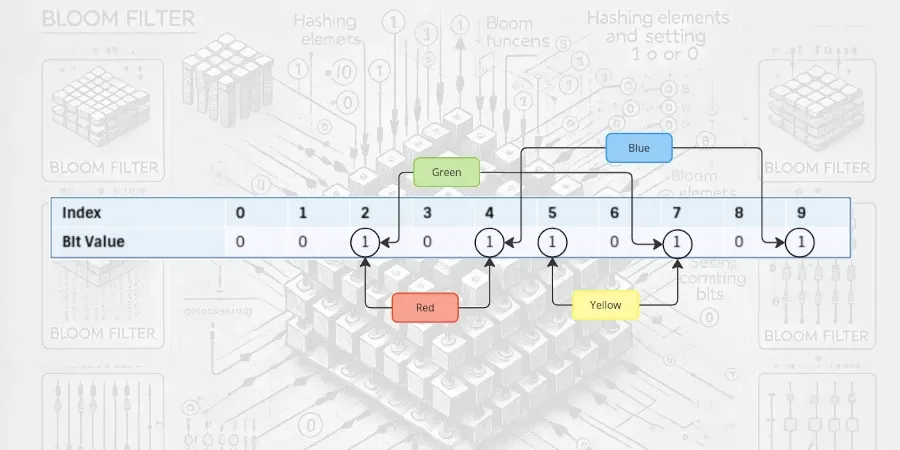
Let's work through an example where we'll use a bloom filter of 10 bits and two hash functions – h0 and h1.
If we want to determine if we have seen the element "red" before, we can run this through both hashing functions to determine the bit indexes for us to check within the bloom filter.
h0("red") (mod w) = 2
h1("red") (mod w) = 5
Because our bloom filter is a fixed width, we have to ensure the hashed value is constrained to the width of the array using modular arithmetic.
Because 2 and 5 are set to 0 in our bloom filter, we know definitively that we have not seen these before, and we can set these values to 1, to indicate that we have now seen the element "red".
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Bit Value | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
If we were to consider another element, "blue":
h0("blue") (mod w) = 4
h1("blue") (mod w) = 9
Bits 4 and 9 are both set to 0, so we know we haven't seen "blue" before.
We can now set these new bits to 1 to track that we have now seen blue.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Bit Value | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
If we were to consider another element, "yellow":
h0("yellow") (mod w) = 5
h1("yellow") (mod w) = 7
Bit 5 is set to 1, but bit 7 is set to 0, so we know that we haven't seen "yellow" before.
We can now set these new bits 7 to 1 to track that we have now seen yellow.
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Bit Value | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
Finally, if we were to consider another element, "green":
h0("green") (mod w) = 2
h1("green") (mod w) = 7
Both 2 and 7 have already been set to 1, so we've probably seen "green" before. In this specific instance, we're picking up the 2nd bit from red and the 7th bit from yellow.
This can occur because hash functions are typically imperfect, and they can generate the same hash value for different keys that are passed to them — this is known as a hash collision.
Due to the finite size of a bloom filter and the nature of hash functions, a bloom filter will have collisions where more than one value can correspond to the same series of bits. This is why a bloom filter will have a false positive rate and cannot definitely determine if an element is a member of the set. On the other hand, it is impossible for a bloom filter to have a false negative response.
The Size of a Bloom Filter
Four factors ultimately control the size of a bloom filter:
- The number of items that the filter should be able to hold
- The probability of false positives
- The number of bits in the filter
- The number of hash functions
Typically, you can use a bloom filter calculator to determine the appropriate values for these attributes. By providing 2 or 3 of these attributes (e.g. number of items and probability of false positives), it is possible to calculate and determine the remaining attributes, such as the size of the filter and number of hash functions required.
Use Case In-Depth
Several well-known use cases that demonstrate the benefits that a bloom filter can bring to applications and data sets at scale.
Google Safe Browsing
Google Chrome can identify and warn users of a malicious site before visiting it. In principal, you would expect that Chrome checks the URL a user is about to visit against a database of malicious URLs.
The problem with this approach is that there could be a lot of malicious URLs out there, making a database of malicious URLs quite large. Distributing a large database with a day-to-day application like a web browser would be undesirable. Google would also want to avoid having to make an external API call or depending on an external service to determine if a URL is malicious – given that they have a large user base of over 3.46 billion users.
The Google Chrome team avoided these challenges by using a bloom filter. A bloom filter will be considerably smaller than a more traditional database. Chrome uses the bloom filter to determine if a URL is malicious.
The bloom filter will be able to rule out non-malicious URLs without any risk of a false negative. The bloom filter will respond "probably yes" if the URL is malicious or if the URL has been incorrectly identified as a false positive.
Anecdotally, the set of non-malicious URLs will be substantially larger than the set of malicious URLs. Therefore, a bloom filter works well to rule out non-malicious content. If the bloom filter determines a URL may be delicious, there are then two choices:
- Incorrectly warn the user that the URL may be malicious when it isn't, or
- Call out to an external API or service to deterministically check if the URL is malicious
This approach of using a bloom filter has several advantages:
- There is no need to distribute a large database or malicious URLs; instead, a much smaller bloom filter can be distributed with the browser
- Bloom filters are typically very fast therefore the user will not notice any performance degradation as a result of these safe browsing checks
- The bloom filter can reduce the number of requests/URLs that may require a more expensive, deterministic check to just those that are malicious and may be subject to false positives.
As a basic comparison, if we were to have a basic data structure of one million malicious domain names that we could check without any false positive risk, this would require roughly ~15MB of storage.
If we were to use a bloom filter, we could do this with just 2.8MB of storage, but allowing for the fact that we would have a false positive for every 1 in 100,000 queries. The storage saving is significant for the small trade-off of a 1 in 100,000 false positive rate.
Akamai Cache Performance
A Content Delivery Network (CDN) works by caching content at edge nodes in a network so that content can be returned to a user without having to query the origin server. CDNs typically reduce the load on origin servers and improve the speed of web pages by caching content closer to the user at the edge of the CDN.
When a CDN is queried for a web page or an asset, it will serve this up from its cache, provided the item exists in the cache. If, however, there is a "cache-miss" and the item does not exist in the cache, the CDN will:
- Request the page/asset from the origin server
- Cache it in the network for subsequent requests
- Return the page/asset to the requester
This behaviour typically means that the first time a page or asset is requested from a CDN, the request will have to go back to the origin to populate the cache, but any subsequent requests can be served directly from the CDN cache.
Akamai found that 75% of their cached assets consisted of one-hit-wonders – assets that have only been requested once. As a result, a lot of cache storage was being taken up by content that didn't need to be cached because it wasn't being accessed repeatedly.
Akami elevated this issue by introducing a bloom filter. The bloom filter was used to determine if an asset had been requested before:
- If the answer is definitely no, then there is no need to cache the asset as this is the first (and potentially only) time that the asset is being requested.
- If the answer is probably yes, then the asset has more than likely been requested before, and we should cache it.
This is an excellent application of a bloom filter because the benefits for Akami are significant, and even in the event of a false positive, the end user will experience no adverse behaviour.
In the event of a false positive, Akamai will cache a page in their CDN that will only be accessed once. As far as the user is concerned, they'll see no impact or perceivable difference in the CDN service. There is a minor disadvantage that Akami will cache a few one-hit-wonders that will correlate to the false positive probability of their bloom filter. However, the bloom filter allowed them to cut down the persisted cache size to eradicate nearly all 75% of the one-hit wonders.
Articles You've Read
Medium uses a per-user bloom filter to track which articles a user has read. On the surface, this sounds simplistic, but why wouldn't you use a relational database to track this?
Whilst Medium does not publish official stats on the total number of articles or the total number of members that they have, with a website ranking within the top ~150 websites in the world, it is fairly safe to assume that both of these figures will be substantial, and as a result, any database table tracking who has read what would require a significantly amount of storage.
A bloom filter offers a much more space-efficient way to store and query this information. And whilst a probabilistic data structure is not 100% accurate, the risk of a false positive is very slim – as Medium would risk showing an article to a user they've not read before. If this happened all the time, it would be problematic, but if it happens occasionally, would a user notice or even care? Probably not.
This Medium example also demonstrates that a problem can be solved with multiple bloom filters. A single bloom filter on its own won't allow you to determine which user has read what article, but if you have a bloom filter per user, then you can determine if a given user has (likely) read a particular article.
Anonymous Database
Another consideration for a bloom filter is if you ever need to test "is an element a member of the set" without distributing the explicit database.
If it were possible to determine which element corresponded to which bits, then a bloom filter wouldn't be probabilistic and wouldn't be subject to a false positive rate.
As a result, this means that a bloom filter may apply to use cases where you want to perform a set membership test but without distributing the underlying dataset.
Naturally, a false positive may occur, and the best way to handle this will be subject to the specific conditions of the use case. The likelihood of this happening will depend on the configuration of the bloom filter.
Duplicate Detection and Data Retention
Given that, a bloom filter is designed to answer the question:
Is a given element a member of a set?
Bloom filters are well suited to detecting duplicates or if an item has been seen before.
Determining if a duplicate data record has been seen before is often expensive on storage, because it means that you have to retain either the entire record or some deterministic fingerprint for every record you have ever seen.
This can cause issues because data has to be retained indefinitely, which means the dataset will typically grow linearly over time.
Alternatively, a bloom filter could detect duplicates without retaining data indefinitely – allowing for some caveats and limitations.
Remember that a bloom filter is preconfigured to a deterministic size. Therefore, you will need to assume how much data you want the filter to retain for it to be effective, but it does mean that you could have duplicate detection beyond a retention period.
For example:
- We may have a 90-day retention window for bug reports delivered over a bug reports API.
- We want to detect duplicates so that they can be discarded to prevent duplication and wasted effort.
In this scenario, we could, for example, configure a bloom filter that may allow for five years of bug reports to be stored in the filter. Whilst we would have to deal with the issue of the filter becoming saturated in five years, this would allow us to perform duplicate detection beyond the retention window and without violating the retention policy.
Conclusion
Designing and operating systems and datasets at scales often involves trade-offs. Probabilistic data structures such as bloom filters provide a highly performance space-efficient way of determining if an item belongs to a set – provided we can tolerate an element of false positive.
As we have seen from the examples we explored as part of this explanation, bloom filters can be used when the risk of a false positive is inconsequential. A false positive may be more problematic in other scenarios. However, confirming positive answers from a bloom filter by making a more expensive call to an external service or deterministic data source may be a warranted trade-off. Equally, there are use cases where a bloom filter would be entirely inappropriate.
For the right problem, a bloom filter can be the correct trade-off.